算法:Sequence Search
站内链接:
- 算法(1)-检索-简介
- 算法(2)-检索-散列检索
- 算法(3)-检索-顺序检索
- 算法(4)-检索-树检索
- 算法(5)-排序-简介
- 算法(6)-排序-分配排序
- 算法(7)-排序-插入排序
- 算法(8)-排序-选择排序
- 算法(9)-排序-交换排序
- 算法(10)-排序-外排序
Introduction
Intro
线性搜索或顺序搜索是一种寻找某一特定值的搜索算法,指按一定的顺序检查数组中每一个元素,直到找到所要寻找的特定值为止。是最简单的一种搜索算法.
线性搜索在物理上可以顺序, 也可以连接, 但是逻辑上是顺序存储的. 相比哈希检索, 线性检索的数据没有任何限定, 没有额外的键值空间消耗, 没有唯一值的限定.
Classify
- 无序表查找: 数据本身没有经过排序, 通过暴力遍历查找数据
- 有序表查找: 二分查找, 差值查找, 斐波那契查找, 线性索引查找
Order Search
Analysis
检索过程: 针对线性表里的所有记录,逐个进行关键码和给定值的比较
- 若某个记录的关键码和给定值比较相等,则检索成功
- 否则检索失败
物理存储: 在物理上可以顺序, 也可以链表存储, 但在逻辑上是顺序存储的
性能分析
使用暴力搜索, 时间复杂度: O(n)
Example
1 | def sequential_search(lis, key): |
Binary Search
Analysis
数据本身在存储或者取出时, 必须先经过排序, 以便在后续的搜索过程中能够更加方便快捷. 一般而言, 在搜索算法中, 都要求数据为静态数据, 不会经常性的进行数据的更新和删除操作. 对于大数据, 如果使用暴力搜索, 性能可能不如想象, 在对已排序数据进行查找时, 则有多种方式:
- 二分查找: 查找表中不断比较中间元素与查找值,以二分之一的倍率进行表范围的缩小
- 插值查找: 对半过滤还不够狠, 如果以 10 分之 9 的倍率进行范围缩小, 能够更快的进行缩减, 使用
value = (key - list[low])/(list[high] - list[low])公式来完成 - 斐波那契查找: 利用斐波那契数据列表降低搜索范围
性能分析
时间复杂度: O(logn)
Example
1 | def binary_search(lis, key): |
Blocking Search
Analysis
顺序索引查找, 这是顺序和二分法的折衷, 既有较快的检索, 又能保证灵活的更改.
基本思路: 按照块有序来进行数据排序, 其中块中的关键码并非有序的, 其中索引表记录了各个块中的最大关键码以及各个块的起始位置, 相当于 C 中的指针概念.
索引表: 一个递增有序的表结构
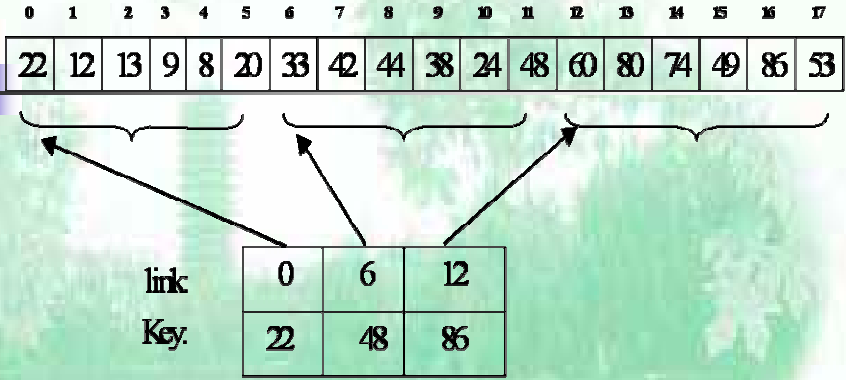
性能分析
时间复杂度: ASL(n) = ASL(b) + ASL(w)
索引表是顺序表: ASL = n^(-2)
索引表是二分: ASL = log2(1 + n/s) + s/2
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 狂想写作本!
评论