算法:Hash Search
站内链接:
- 算法(1)-检索-简介
- 算法(2)-检索-散列检索
- 算法(3)-检索-顺序检索
- 算法(4)-检索-树检索
- 算法(5)-排序-简介
- 算法(6)-排序-分配排序
- 算法(7)-排序-插入排序
- 算法(8)-排序-选择排序
- 算法(9)-排序-交换排序
- 算法(10)-排序-外排序
Introduction
Intro
参考搜索算法的介绍.
散列检索, 用以提高检索效率, 大部分情况下是面向用户的操作, 根据用户的输入来进行快速的检索, 并尽可能快速的给出结果. 在这种要求下, 如何存储数据? 以怎样的结构来构造?如何避免冲突?如何解决检索的唯一性? 这些都是散列检索需要解决的问题.
Classify
- 静态索引: 在初始阶段, 索引结构已经固定下来, 整个存储结构是固定的
- 动态索引: 在系统运行过程, 索引本身会一直在变化
性能分析
平均检索长度: 决定了查找的性
负载因子: a = N/M, 其中 N 表示源数据, M 表示散列表存储空间, 其中 a 越大, 则表示发生冲突的可能性越高, 很多记录偏离基地址的可能性越大.
B-tree
Intro
B-tree 的提出基于以下的背景:
1 | 对于大规模的数据存储, 如果使用二叉查找树, 那么该存储 |
B-tree: 保持树结构较低的高度, 避免磁盘过于频繁的查找存取操作(同一个节点里面的 key 可以顺序存储在磁盘上), 有效的提高检索效率. 实际上, 每个结点包含大量的关键字信息和分支, 当然不能超过磁盘块的大小(一般为 1k~4k), 这样根据磁盘读取的原理, 每次读取一个磁盘块就相当于读取一个结点, 大大的提高效率.
B-tree 定义(m 分叉):
- 根节点至少包含两个子节点, 除非仅仅存在一个根节点
- 每个节点至多有 m 个子结点, 每一个内结点至多有[ceil(m/2)]个孩子(向上取整).
- 所有的叶子结点都处于相同的深度
- 如果某一个内结点(非 root, 非叶子), 若该结点含有 s 个键值, 那么该结点一定存在 s+1 个子节点
检索
根节点读出并将其中关键码与查找值比较
- 如果找到, 则检索成功
- 否则找到当前结点 ki~ki+1 之间的 pi, 进入子树
重复上述步骤, 递归, 知道找到或者 pi 为空(叶子结点)时停止
如果树高为 h, 则需要 h 次读索引盘 + 由关键码中隐含指针找到记录主文件位置的一次读盘
插入
检索是否存在, 如果存在, 直接决绝, 返回索引位置__
最后定位的叶子结点为待插入的位置
插入完成后
- 叶子结点关键码个数小于 m, 则插入完成, 直接返回__
- 叶子结点关键码个数等于 m, 产生上溢出(key 过多), 取这 m 个关键码的中位数, 分裂为左右孩子
将中位数分解码插入到父节点中, 如果父节点未上溢出, 则返回__
继承上面的步骤, 一直往根节点递归传递, 其中根节点允许的子结点数在 2~m-1 之间.
删除
- 如果删除的关键码 x 不在叶节点层, 则将此关键码与后继结点对换位置, 即将右指针子树中的最左的叶子结点提到当前位置, 同时删除 x.
- 如果删除后产生下溢出(最小元素数目为 ceil(m/2)), 需要向父节点借一个节点, 将最丰满的相邻兄弟结点中上移最后或最前一个元素到父节点中(类似左旋操作).
删除 R 元素:
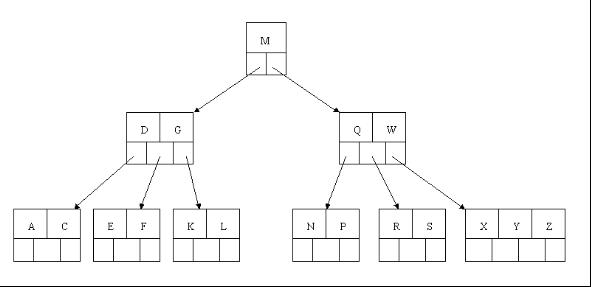
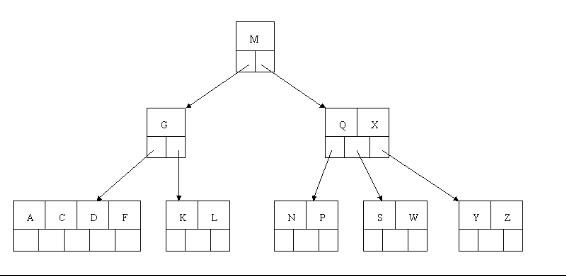
调整, W 下移, X 上移:
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 狂想写作本!
评论