算法：External Sort

站内链接:

Introduction

Intro

外排序: 利用外部文件进行排序的技术, 用以解决内存不足或者数据量过大的问题, 整个外排序过程如下:

对单个文件进行排序, 其中排序算法一般是内排序, 在内存中进行
逐趟对多个有序文件进行归并操作
最终形成一个有序的唯一文件

外排序总耗时统计:

内排序使用时间
磁盘信息的读/写时间
在将数据写入内存并进行归并排序的时间

外排序总耗时优化:

减少初始有序文件的个数(K)
增加归并的有序文件数量, 使用多路归并排序算法

文件管理

文件是一种存储在外存上的数据结构, 它由大量性质相同的记录组成.

操作系统文件: 一组连续的字符序列, 无明显的顺序
数据库文件: 有结构的记录集合
单关键码文件/多关键码文件: 定长/不定长文件

文件组织

逻辑组织:

顺序结构的定长记录
顺序结构的变长记录
按关键码存取的记录

物理组织:

顺序文件: 磁带
散列文件: 适合随机存取, 无法顺序存取
索引文件: 顺序文件, 根据索引来存取
倒排索引: 用记录的非主属性值(副键)来查找记录而组织的文件, 次索引(倒排)文件

置换选择

Requirement

置换选择排序的提出目的: 解决磁盘 IO 和内存性能之间的差距问题, 用以解决对某一个大文件进行排序的问题, 对于一个内存为 N GB 的机器, 可以将文件转换为大概 2N 的顺序串, 从而达到减少 K 的目的, 减少外排序的性能.

Analysis

根据上章内容可知, 为了降低外排序的耗时, 需要减少归并趟数, 其中归并路数 k, 归并端的个数 n, 影响到归并趟数.
置换-选择排序就是一种减小 n 的, 在外部排序中创建初始归并段时用到的算法, 它可以让初始归并段的长度增减, 从而减小初始归并段的段数. 一般使用败者树或者赢者树来进行置换-选择算法的实现.

整个数据的读写过程如下: input file-->buffer-->Memory-->buffer-->output file. 详细过程(对于内存为 N 的机器):

1. 从输入文件读取N 个数字, 构建最小堆
2. 重复下面步骤, 直到堆的大小为0:

    a. 把根结点的数字A（即当前数组中的最小值）输出
    b. 从输入文件中再读出一个数字B, 若R比刚输出的数字A 大，则将B放到堆的根节点处，若B不比A大，则将堆的最后一个元素移到根结点，将B放到堆的最后一个位置，并把堆的大小缩减1
    c. 调整堆结构

3. 重复上面的所有步骤, 将输出重定向到另外一个文件

Example

import heapq
import random


class HeapSorter(object):
    def __init__(self, num_blocks, input_sequence):
        self.num_blocks = num_blocks
        self.input_sequence = input_sequence

    def sorted(self):
        # 堆排序模块heapq.
        # merge: 归并排序
        return heapq.merge(*self.__sorted_subsequences__())

    def __sorted_subsequences__(self):
        """
        构建多个有序列, 每一次yield返回有序列表
        """
        # Initialization: read B pages into the current_heap
        current_heap = [self.input_sequence.pop(0) for x in xrange(self.num_blocks)]
        # 将list(current_heap)变为一个堆结构, 更改原始列表(完全二叉树)
        # 对于下标i元素, 其左右子节点的下标: 2*i+1, 2*i+2
        heapq.heapify(current_heap)
        next_heap = []
        current_run = []

        while current_heap:
            # 首先从堆内存中获取最小值并存入current_run
            lowest = heapq.heappop(current_heap)
            current_run.append(lowest)

            # 其次, 每一次输出之后, 重新获取未排序值放入败者树中
            if self.input_sequence:
                next_element = self.input_sequence.pop(0)
                # 将next_element压入对败者树中, 此时如果next_element小于
                # current_run中的最大值(lowest), 则推入next_heap
                heapq.heappush(current_heap if next_element >= lowest
                               else next_heap, next_element)

            # 每次current_heap为空就表示当前已经构建了一个列表, 并且此时
            # next_heap中的所有值都小于current_run中最大值
            if not current_heap:
                current_heap, next_heap = next_heap, current_heap
                yield current_run
                current_run = []


if __name__ == "__main__":
    # 初始化待排序数值列表
    sorter = HeapSorter(10, [random.randrange(10000) for x in xrange(100)])
    # 排序
    print(list(sorter.sorted()))

二路外排序

Intro

基于分治算法, 结合归并排序和多路归并排序, 这里不再做深入说明.

Example

import time
import sys

def Merge(array, low, middle, high):
    # 左有序队列长度
    n1 = middle - low + 1
    # 右有序队列长度
    n2 = high - middle
    left_array = []
    right_array = []

    # 把array 左边的值，放到left_arr  数组里面
    left_array = [array[i + low] for i in range(0, n1)]
    # 把 array 右边的值，放到 right_arr  数组里面
    right_array = [array[j + middle + 1] for j in range(0, n2)]

    i, j = 0, 0
    k = low
    while i != n1 and j != n2:
        if left_array[i] <= right_array[j]:
            array[k] = left_array[i]
            k += 1
            i += 1
        else:
            array[k] = right_array[j]
            k += 1
            j += 1

    while i < n1:
        array[k] = left_array[i]
        k += 1
        i += 1

    while j < n2:
        array[k] = right_array[j]
        k += 1
        j += 1


def MergeSort(array, p, q):
    """分治, 不断的分解, 再自下而上归并"""
    if p < q:
        # 转成int  类型
        mid = int((p + q) / 2)
        MergeSort(array, p, mid)
        MergeSort(array, mid + 1, q)
        Merge(array, p, mid, q)

败者树/胜者树

Intro

败者树和胜者树都是完全二叉树, 其中:

叶子结点相当于一位选手
中间结点相当于一场比赛
每一层相当于一轮比赛, 几乎是归并排序的天然表现, 只不顾目的和结果不同罢了

其中任何一个叶子结点值的改变, 都会利用中间节点, 自下而上, 经过 log(n)快速的找到当前组中的新的最值. 其中胜者树的中间结点记录的是胜者标号, 败者树的中间结点记录的是败者标号.

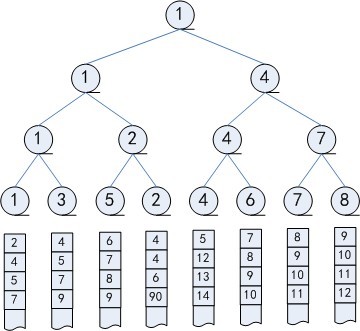
败者树在 k 路排序

利用败者树, 在 k 路排序中经常用到, 从而快速的进行排序操作, 具体流程如下:

loser tree

整个过程如下:

利用置换选择排序, 将一个大文件分成多个排序后的小文件
利用败者树进行多路归并排序

多路归并排序

Analysis

根据第一章的说明可知, 对于外排序, 增大 k(路数)有助于提升外排序性能, 其中计算方式如下, 对于 k 路, 对 n 个记录的文件, 归并趟数 s, 在总的比较次数:

s * (n-1) * (k-1)
对于任何一条记录: 需要比较k-1次, 才能提取最小值
对于n个记录的文件: 总共需要(n-1) * (k-1)次数比较
对于m个归并段, s=logkm: 总共需要logkm * (n-1) * (k-1)

将该值进行向上取整: log2m/log2k * (k-1) * (n-1)

此时可知, 随着 k 的增加, 整体的内部排序次数增加, 从而抵消了多路排序一开始提出的时间优势, 所以提出了 tree of loser 概念.

Example

import heapq

def kmerge(iterables, keyFcn=None):
    _heappop, _heapreplace, _StopIteration = heapq.heappop, heapq.heapreplace, StopIteration
    # 用于生成迭代器的函数
    _iter = iter

    h = []

    # 1 利用map函数式编程函数, 对iterables中所有列表进行转换, 返回一个生成器列表
    for itnum, it in enumerate(map(_iter, iterables)):
        try:
            next = it.next
            if keyFcn is not None:
                h.append([keyFcn(next()), itnum, next])
            else:
                h.append([next(), itnum, next])
        except _StopIteration:
            pass

    # 2 这里利用生成器来进行一次次进行归并排序, 此时h中存储了所有k路的所有
    #   首位记录
    heapq.heapify(h)

    while True:
        try:
            while True:
                v, itnum, next = s = h[0]   # raises IndexError when h is empty
                yield v

                if keyFcn is not None:
                    s[0] = keyFcn(next())
                else:
                    s[0] = next()       # raises StopIteration when exhausted
                _heapreplace(h, s)          # restore heap condition
        except _StopIteration:
            _heappop(h)                     # remove empty iterator
        except IndexError:
            return


if __name__ == '__main__':
    x = kmerge([
        [1, 3, 5, 7],
        [0, 2, 4, 8],
        [5, 10, 15, 20],
        [],
        [25]
    ])
    for i in x:
        print i,
    print