站内链接:
Introduction 选择排序, 直接从源中选择一个最大/最小的值, 并在结果序列中进行尾部插入操作.
直接选择排序: 从数组 A[n]中选择最大值, 放在目标尾部
堆排序: 从数组 A[n]中选择最大值, 放入到最大值堆中
归并排序: 从 n 个子序列中, 选择一个最大值放入目标尾部, 递归进行
直接选择排序 Anaylysis
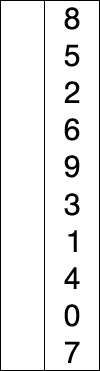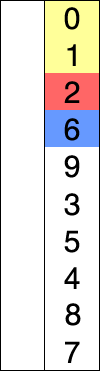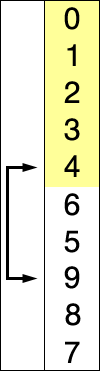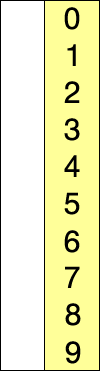
首先, 未排序序列中找到最小(大)元素,存放到排序序列的起始位置
然后,从剩余未排序元素中继续寻找最小(大)元素, 放到已排序序列的末尾
以此类推,直到所有元素均排序完毕.
选择排序的最优解: 如果某数位于正确的位置, 那么将不会有移动开销. 选择排序本身并非一个稳定的排序算法, 对于逆序的组合, 极端情况下达到 O(n^2) 复杂度
Example 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def selectSort (list1 ): """selectSort: :param list1:source list1 """ list_len = len (list1) for i in range (0 , list_len)[::-1 ]: maxIndex = i for j in range (0 , i): if list1[j] > list1[maxIndex]: maxIndex = j list1[maxIndex], list1[i] = list1[i], list1[maxIndex] return list1
堆排序 Analysis 堆(二叉堆)是一棵完全二叉树, 从而可以使用数组来表示整个堆结构, 当然, 如果是普通的二叉树, 则使用链表来进行数据的存储. 本质上,一种比较类-非线性-选择类-排序. 近似完全二叉树:
1 2 3 4 5 6 7 8 9 堆性质: ki <= k2i 并且 ki <= k2i + 1 或者 ki >= k2i 并且 ki >= k2i + 1 其中(1 <= i <= n/2) 二叉堆性质: value(父节点) >= value(子节点) 任何一个子树都是一个二叉堆
最大根堆进行排序操作:
交换 R[1]和 R[n],人工构建了一个非堆结构,重建堆 R[1…n-1];
交换 R[1]和 R[n-1],重建堆 R[1…n-2],有序堆 R[n-1..n];
不断的作死,不断的修补,最终得到一个最小堆结构;
如果要得最大堆,交换 R[n]和 R[i],重建堆 R[i+1..n],有序堆 R[1..i];
为何是选择排序类别: 不断的自我作死,选择出最大的根节点放在合适的位置上. 游戏开始,我是裁判:
1 2 3 4 5 你们,组一个大根堆! n秒后,来,最天才的,站我旁边 你们,剩余的n-1的SB,再组一个大根堆 n秒后,来,最天才的,站在刚才最最天才的旁边 .....唉
双堆结构(最小堆、最大堆)可以用来维护中位数:
首先,它是一个完全二叉树
其次,左堆是一个最小堆
再次,右堆是一个最大堆
再再次,左堆小于根(中位数),右堆大于根
然后就 OK 了,怎么有点像二叉查找树?
Example 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 def moveDown (list1, start, end ): """moveDown:调整堆结构 :param list1: :param start:heap min edges :param end:head max edges """ largest = 2 * start + 1 while largest <= end: if (largest < end) and (list1[largest] < list1[largest + 1 ]): largest += 1 if list1[largest] > list1[start]: list1[largest], list1[start] = list1[start], list1[largest] start = largest largest = 2 * start + 1 else : return def create_heapify (list1, list_len ): """create_heapify:创建初始堆 :param list1: :param list_len: """ first = int (list_len / 2 - 1 ) for start in range (first, -1 , -1 ): moveDown(list1, start, list_len - 1 ) def heap_sort (list1 ): """heap_sort:sort :param list1: """ list_len = len (list1) create_heapify(list1, list_len) for end in range (list_len - 1 , 0 , -1 ): list1[end], list1[0 ] = list1[0 ], list1[end] moveDown(list1, 0 , end - 1 ) return list1
归并排序 Analysis 本质上,一种比较类-非线性-归并类-分治思想-排序. 将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。归并排序有多路归并排序、两路归并排序 , 可用于内排序,也可以用于外排序. 自顶向下-分治思想:
步步为营,各个击破,大问题分解为若干小问题,最后组合。
从一开始就自上而下,首先经过顶层,最后才到底层。
空气干燥 –> 草原可能会发生大火 –> 各处的星星之火
自底向上思想:
在一种大的约束下,但是推导时没有考虑合并后的操作,
我们先干自己的,合并邻居,之后再说。
星星之火,哪有志气和心情去燎原!
分类:
内排序:内存中的排序(归并、快排、堆排序、基数)
外排序:将文件分块放入内存,之后对内存中数据排序,写回文件
流程:
把 n 个记录看成 n 个长度为 l 的有序子表
进行两两归并使记录关键字有序,得到 n/2 个长度为 2 的有序子表
重复第 2 步直到所有记录归并成一个长度为 n 的有序表为止
Example 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 def merge (left, right ): """merge:merge left and right. Notes, left and right are ordered list. :param left: :param right: """ lindex, rindex = 0 , 0 left_len = len (left) right_len = len (right) result = [] while lindex < left_len and rindex < right_len: if left[lindex] < right[rindex]: result.append(left[lindex]) lindex += 1 else : result.append(right[rindex]) rindex += 1 result += left[lindex:] result += right[rindex:] return result def mergeSortDC (list1, left, right ): """mergeSortDC:自顶向下,采用递归方式,分治法思维: 步骤: 分解:将当前区间分解,分裂点(low+higth)/2下边界 求解:递归的堆[low..mid]和[mid+1..high]进行归并排序 组合:将上面已经排序的[low..mid]和[mid+1..high]进行merge操作 PS:递归的终结条件为1 :param list1: """ if left >= right: return list1[left:right + 1 ] num = (left + right) / 2 left_list = mergeSortDC(list1, left, num) right_list = mergeSortDC(list1, num + 1 , right) return merge(left_list, right_list)